【連立方程式】 分母の数が大きい場合の計算
中学生からの質問（数学）
連立方程式の文章題を解くときに，分数がたくさん出てきます。分母が大きい分数の計算が苦手なのですが，何かコツはありますか。
分母の最小公倍数を見つけ，両辺にかけます。
見つからない場合は，分母の数を全部両辺にかけてもよいです。
- ● 分母の最小公倍数を見つけ、両辺にかけます。
- [例]
+ 
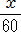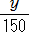＝16
最小公倍数の見つけ方 … 150，150×2＝300，150×3＝450，…というように大きい方の数の倍数を計算し，小さい方の数 60 でわり切れるか確認していきます。
60 と 150 の最小公倍数は 300 なので，両辺に 300 をかけます。
（
+ 
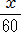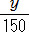）×300＝16×300
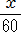×300 + 
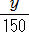×300＝16×300 より，5x + 2y＝4800
- ● 最小公倍数を見つけられない場合は，分母の数を全部両辺にかけてもよいです。
-
（
+ 
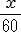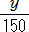）×60×150＝16×60×150
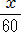×60×150 + 
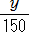×60×150＝16×60×150 より， 150x + 60y＝144000 - ● できるだけ小さな整数で計算していく方がラクでミスも防げます。
-
[例]
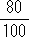x +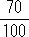 
y＝5000
両辺に 100 をかけて整数に直し，連立方程式を解いていってもかまいません。
（
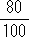x +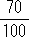 
y）×100＝5000×100 より，80x + 70y＝500000
また，元の式の左辺をみるとどちらの項も 10 で分子・分母を約分できて，少し式が簡単になるのがわかります。よって両辺に10をかければよいのです。
（
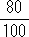x +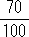 
y）×10＝5000×10 より，8x + 7y＝50000
