【１次方程式】何をｘにすればよいのか

中学生からの質問（数学）

『みかんを何人かに，1人6個ずつ分けると3個余り，7個ずつ分けると8個たりないとき，人数とみかんの個数を求めなさい。』というような問題で，何をｘにすればよいかわかりません。

何をｘとするかは， 1とおりではありません。ｘの決め方によって，立てる

方程式が異なります。多くの場合，求めるもの（2つ以上ある場合はどれ

か1つ）をｘとして，問題の中の数量をｘを使って表します。

[例]　みかんを何人かで分けるのに，1人に6個ずつ分けると3個余り，1人に7個ずつ分けると8個たりない。人数とみかんの個数を求めなさい。

この問題では，求めるものが2つ（人数とみかんの個数）あるので，一方をｘとし，もう一方をｘを使った式で表します。

（解き方1）　人数をｘ人とした場合，みかんの個数をｘを使った式で表すと，

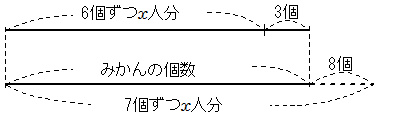（みかんの個数）＝6ｘ+3（個）

（みかんの個数）＝7ｘ-8（個）

分け方によらず，みかんの個数は同じだから，方程式は6ｘ+3＝7ｘ-8

これを解くと，ｘ＝11　人数は11人となります。みかんの個数は，ｘ＝11を6ｘ+3に代入して

6×11+3＝69（個）となります。

（解き方2）　みかんの個数をｘ個とした場合，人数をｘを使った式で表すと，

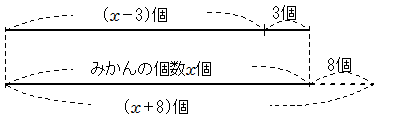（人数）＝（人）

分け方によらず，人数は同じだから，解くべき方程式は
これを解くと，ｘ＝69　みかんの個数は69個となります。人数は，ｘ＝69をに代入して

（69-3）÷6＝11（人）となります。

以上のように，ｘの決め方によって，解くべき方程式がかわることに注意しましょう。

進研ゼミ　LINE公式アカウント友だち募集中！アカウント連携でLINEポイント100ポイントプレゼント

中学生からよく聞かれる質問（数学）

⇒すべての質問を見る

▼ほかの教科を見る

詳しい講座の紹介はこちらから

まずは、お子さまの学年をお選びください。

「進研ゼミ　ハイブリッドスタイル」はお手持ちのiPadでご利用いただけます。

対応機種
iPad（第4世代）、iPad Air、iPad Air 2、iPad mini 2、iPad mini 3、iPad mini 4

通信環境
常時接続可能なブロードバンド（光ファイバなど）環境と、無線LAN（Wi-Fi）環境をご用意ください（10Mbps以上を推奨）。ご利用環境の通信速度については、下記より事前にご確認ください。回線チェック開始

上記に合致しない環境では、サービスをご利用いただけない場合があります。
インターネットサービスプロバイダとの契約、無線LANルータが必要となります。接続料金等はお客さまのご負担となります。
セルラーモデルのiPadをご利用の方も、無線LAN(Wi-Fi)環境が必要です。ただし、テザリング機能での通信は推奨いたしません。

地域／受付時間	～13時まで	13時以降～
北海道・東北・沖縄県・その他一部の地域	2日前後	3日前後
上記以外の地域	翌日	2～3日前後

地域／受付時間	～13時まで	13時以降～
北海道・東北・沖縄県・その他一部の地域	2日前後	3日前後
上記以外の地域	翌日	2～3日前後

地域／受付時間	～13時まで	13時以降～
北海道・東北・沖縄県・その他一部の地域	2日前後	3日前後
上記以外の地域	翌日	2～3日前後

6か月未満で退会または〈オリジナルスタイル〉に変更の場合、割引分の代金（14,800円税込、消費税率8%）のお支払いが必要です。
6か月以上継続受講で専用端末を無料提供できるのは、1回のみです。
【現在中１・中２生のみ】〈ハイブリッドスタイル〉のご受講は、お手持ちのiPadでも可能です。対応機種はこちら（中学1年生／中学2年生）でご確認ください。iPadシリーズの会員特別優待販売もご用意しています。スペック、販売条件についての詳細はこちら（中学1年生／中学2年生）で必ずご確認ください。
【現在小6生のみ】小5・3月号以前に＜チャレンジタッチ＞を受講されたことのある場合、1月号教材とあわせて、進研ゼミ専用タブレット「チャレンジパッド2」をお届けします。小6・4月号以降に「チャレンジパッド2」をお届けした場合、以前にお届けした「チャレンジパッド2」をご利用ください。新たに代金のお支払いは不要です。お手元にない場合は、お電話でお申し込みください。

※6か月未満で退会または〈オリジナルスタイル〉に変更の場合、割引分の代金（14,800円税込、消費税率8%）のお支払いが必要です。
※6か月以上継続受講で専用端末を無料提供できるのは、1回のみです。
※【現在中１・中２生のみ】〈ハイブリッドスタイル〉のご受講は、お手持ちのiPadでも可能です。対応機種はこちら（中学1年生／中学2年生）でご確認ください。iPadシリーズの会員特別優待販売もご用意しています。スペック、販売条件についての詳細はこちら（中学1年生／中学2年生）で必ずご確認ください。
※【現在小6生のみ】小5・3月号以前に＜チャレンジタッチ＞を受講されたことのある場合、1月号教材とあわせて、進研ゼミ専用タブレット「チャレンジパッド2」をお届けします。小6・4月号以降に「チャレンジパッド2」をお届けした場合、以前にお届けした「チャレンジパッド2」をご利用ください。新たに代金のお支払いは不要です。お手元にない場合は、お電話でお申し込みください。

6か月未満で退会または〈オリジナルスタイル〉に変更の場合、割引分の代金（14,800円税込、消費税率8%）のお支払いが必要です。
6か月以上継続受講で専用端末を無料提供できるのは、1回のみです。
【現在中１・中２生のみ】〈ハイブリッドスタイル〉のご受講は、お手持ちのiPadでも可能です。対応機種はこちら（中学1年生／中学2年生）でご確認ください。iPadシリーズの会員特別優待販売もご用意しています。スペック、販売条件についての詳細はこちら（中学1年生／中学2年生）で必ずご確認ください。
【現在小6生のみ】小5・3月号以前に＜チャレンジタッチ＞を受講されたことのある場合、1月号教材とあわせて、進研ゼミ専用タブレット「チャレンジパッド2」をお届けします。小6・4月号以降に「チャレンジパッド2」をお届けした場合、以前にお届けした「チャレンジパッド2」をご利用ください。新たに代金のお支払いは不要です。お手元にない場合は、お電話でお申し込みください。

キャンペーンの対象は1月号（12/26まで）で〈オリジナルスタイル〉にお申し込みの方と、「チャレンジパッド２」「iPad」など、すでに対応機種をお持ちで〈ハイブリッドスタイル〉にお申し込みの方、対応機種「チャレンジパッド２」をすでにお持ちで〈チャレンジタッチ〉にお申し込みの方となります。対応機種はこちら（小学6年生／中学1年生／中学2年生）でご確認ください。
受講費は1ヵ月分かかります。
2月号以降を継続されない場合は、支払い期間にかかわらず「毎月払い」1ヵ月分の受講費のお支払いとなります。
1ヵ月で退会する場合は1/10までに電話連絡が必要になります。ご連絡はお電話に限ります。
退会連絡をいただかない場合、引き続き２月号以降をお届けします。

※キャンペーンの対象は1月号（12/26まで）で〈オリジナルスタイル〉にお申し込みの方と、「チャレンジパッド２」「iPad」など、すでに対応機種をお持ちで〈ハイブリッドスタイル〉にお申し込みの方、対応機種「チャレンジパッド２」をすでにお持ちで〈チャレンジタッチ〉にお申し込みの方となります。対応機種はこちら（小学6年生／中学1年生／中学2年生）でご確認ください。
※受講費は1ヵ月分かかります。
2月号以降を継続されない場合は、支払い期間にかかわらず「毎月払い」1ヵ月分の受講費のお支払いとなります。
※1ヵ月で退会する場合は1/10までに電話連絡が必要になります。ご連絡はお電話に限ります。
※退会連絡をいただかない場合、引き続き２月号以降をお届けします。

キャンペーンの対象は1月号（12/26まで）で〈オリジナルスタイル〉にお申し込みの方と、「チャレンジパッド２」「iPad」など、すでに対応機種をお持ちで〈ハイブリッドスタイル〉にお申し込みの方、対応機種「チャレンジパッド２」をすでにお持ちで〈チャレンジタッチ〉にお申し込みの方となります。対応機種はこちら（小学6年生／中学1年生／中学2年生）でご確認ください。
受講費は1ヵ月分かかります。
2月号以降を継続されない場合は、支払い期間にかかわらず「毎月払い」1ヵ月分の受講費のお支払いとなります。
1ヵ月で退会する場合は1/10までに電話連絡が必要になります。ご連絡はお電話に限ります。
退会連絡をいただかない場合、引き続き２月号以降をお届けします。

お客さまによりよい教材・サービスをお届けするため、日々改良を重ねております。そのため、ここでご紹介している名称・デザイン・内容・お届け月・アプリの提供期間などは変わることがあります。ご了承ください。最新の情報はWebサイトをご確認ください。
一度退会されて再入会された場合や、スタイル変更をされた場合には、すでに一度お届けしている教材について二度目のお届けをしないものもあります。以前にお届けしているものをお使いください。
「Challenge」「赤ペン先生」、その他当サイトに示す名称は、株式会社ベネッセコーポレーションの登録商標または商標です。

【１次方程式】何をｘにすればよいのか